Repérage sur une droite graduée
Définition :
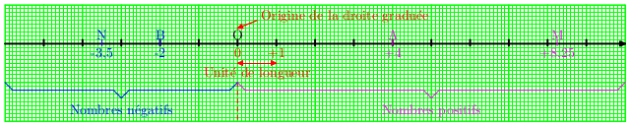
Une droite graduée est une droite sur laquelle on a choisi un sens, un point nommé origine et une unité que l'on reporte régulièrement à partir de l'origine.
À chaque point d'une droite graduée correspond un nombre appelé abscisse.
L'origine O d'une droite graduée a pour abscisse zéro.
La distance de l'origine O à un point d'une droite graduée est appelée la distance à zéro de l'abscisse de ce point.
Exemples :
\(+4\) est l'abscisse du point \(A\). Le point \(A\) est à \(4\) unités de l'origine (\(OA=4\)). La distance à zéro de \(+4\) est \(4\).
\(-2\) est l'abscisse du point \(B\). Le point \(B\) est à \(2\) unités de l'origine (\(OB=2\)). La distance à zéro de \(-2\) est \(2\).