La symétrie centrale
Définition :
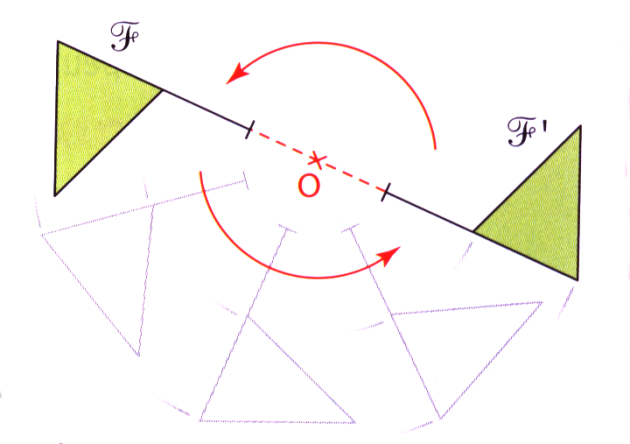
Deux figures sont symétriques par rapport à un point si ces deux figures se superposent lorsqu'on effectue un demi-tour autour de ce point.
Exemple :
Les figures \(\mathcal{F}\) et \(\mathcal{F'}\) sont symétriques par rapport au point \(O\).
Le point \(O\) est le centre de la symétrie.
Propriété :
La symétrie centrale conserve :
les longueurs ;
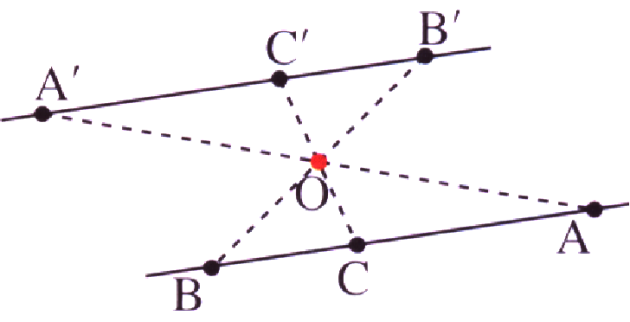
l'alignement ;
les mesures d'angles.
(Cette propriété est héritée de la symétrie axiale ; la symétrie centrale étant équivalente à deux symétries axiales)
Propriété :
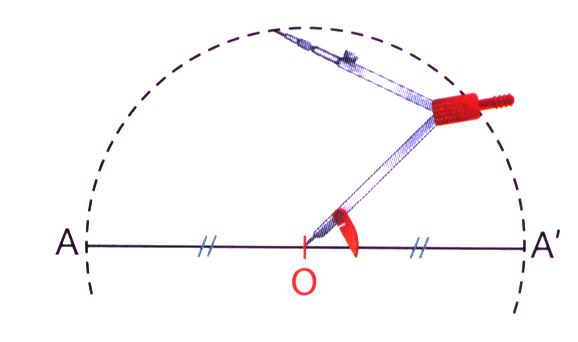
Par la symétrie de centre \(O\), le symétrique :
d'un point \(A\) distinct de \(O\) est le point \(A'\) tel que \(O\) soit le milieu du segment \([AA']\) ;
du point \(O\) est le point \(O\) lui-même.
Propriété :
Le symétrique d'une droite par rapport à un point est une droite parallèle.
Exemple :
\((AB)\) et \((A'B')\) sont symétriques par rapport à \(O\) ; elles sont donc parallèles.
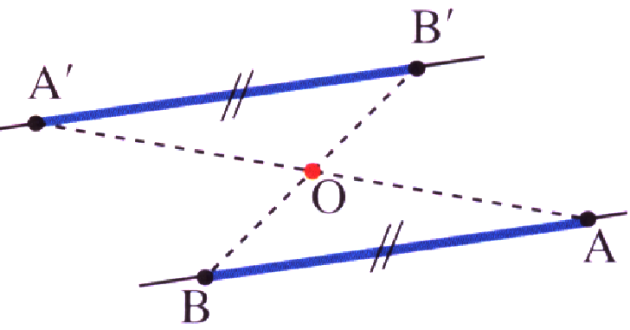
Propriété :
Le symétrique d'un segment par rapport à un point est un segment parallèle et de même longueur.
Exemple :
\([AB]\) et \([A'B']\) sont symétriques par rapport à \(O\) ; \(AB=A'B'\)
Définition :
Un point O est centre de symétrie d'une figure lorsque cette figure est son propre symétrique par rapport à O. On dit que la figure est invariante dans la symétrie de centre O.
Exemple :
La lettre N a un centre de symétrie ; la lettre M n'en a pas.
