Propriétés des angles correspondants et alternes-internes
Propriété :
Si deux droites parallèles sont coupées par une sécante, alors :
les angles correspondants qu'elles déterminent ont la même mesure ;
les angles alternes-internes qu'elles déterminent ont la même mesure.
Exemple :
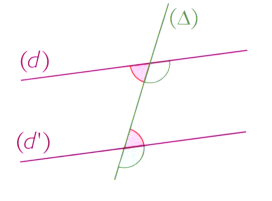
Sur la figure ci-contre, les droites \((d)\) et \((d')\) sont parallèles.
Les angles verts sont correspondants, ils ont donc la même mesure.
Les angles rouges sont alternes-internes, ils ont donc la même mesure.
Propriété :
Si deux droites coupées par une sécante forment deux angles correspondants de même mesure, alors ces deux droites sont parallèles.
Si deux droites coupées par une sécante forment deux angles alternes-internes de même mesure, alors ces deux droites sont parallèles.
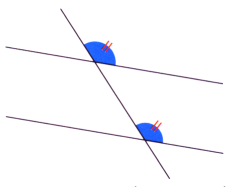
Exemple :
Sur la figure ci-contre, les deux angles alternes-internes sont de la même mesure. Les deux droites coupées par la sécante sont donc parallèles.