La sphère
Définition :
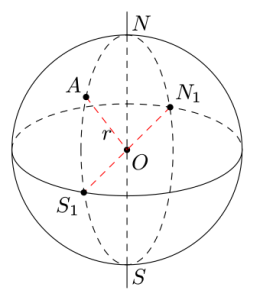
\(O\) est un point de l'espace et \(r\) est un nombre positif donné.
La sphère de centre \(O\) et de rayon \(r\) est l'ensemble des points de l'espace situés à une distance de \(O\) égale à \(r\).
La boule de centre \(O\) et de rayon \(r\) est l'ensemble des points de l'espace situés à une distance de \(O\) inférieure ou égale à \(r\).
Un grand cercle d'une sphère de centre \(O\) et de rayon \(r\) est un cercle de centre \(O\) et de rayon \(r\).
Exemple :
Dans la figure ci-contre :
Le point \(A\) appartient à la sphère de centre \(O\) et de rayon \(r\).
Les points \(A\) et \(O\) appartiennent à la boule de centre \(O\) et de rayon \(r\).
Le cercle de centre \(O\) et de rayon \(OA\) est un grand cercle (\(OA = r\)).
Propriété :
Lorsqu'elle existe, la section d'une sphère par un plan est un cercle, celle d'une boule est un disque.
Illustration
Complément : Calcul de l'aire d'une sphère
Voir la section "Aire d'une sphère" de Grandeurs et mesures->Aire
Complément : Calcul du volume d'une boule
Voir la section "Volume d'une boule" Grandeurs et mesures->Volume