Volume d'un prisme droit ou d'un cylindre de révolution

Propriété

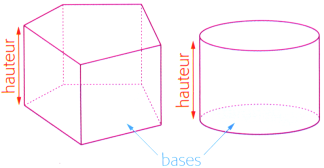
Le volume \(\mathcal{V}\) d'un prisme droit ou d'un cylindre de révolution est le produit de sa hauteur \(h\) par l'aire \(\mathcal{A}_{base}\) d'une de ses bases.

\[\mathcal{V}=\mathcal{A}_{base}\times h\]

Exemples :

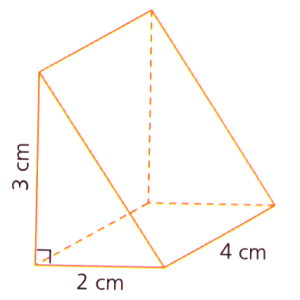
  • Volume du prisme droit représenté ci-dessous :

  • aire d'une base, en \(cm^2\) : \(\mathcal{A}_{base}=\dfrac{3 \times 2}{2}=3\)

  • volume, en \(cm^3\) : \(\mathcal{V}=3\times 4=12\)

Le volume du prisme est égal à \(12~cm^3\).

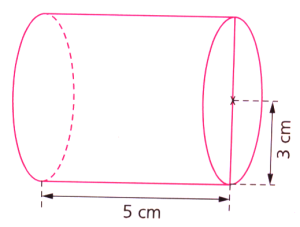
  • Volume du cylindre de révolution représenté ci-dessous :

  • aire d'une base, en \(cm^2\) : \(\mathcal{A}_{base}=\pi\times r^2=\pi\times3^2=9\pi\)

  • volume, en \(cm^3\) : \(\mathcal{V}=9\pi\times 5=45\pi\approx 141,37\)

Le volume du cylindre de révolution est égal à \(45\pi~cm^3\) soit environ \(141,37~cm^3\).