Le cercle circonscrit
Définition :
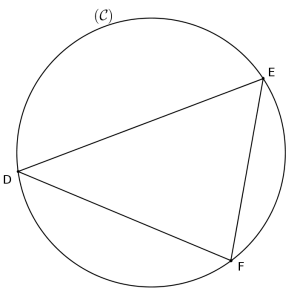
Le cercle circonscrit à un triangle est le cercle passant par les trois sommets de ce triangle.
Exemple :
Propriété :
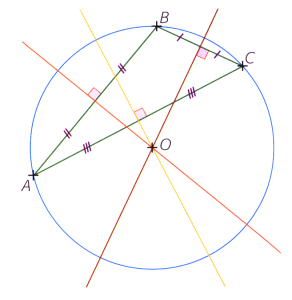
Les médiatrices des trois côtés d'un triangle sont concourantes, elles se coupent en un même point qui est le centre du cercle circonscrit.
Exemple :
Démonstration :
On appelle \(O\) le point d'intersection des médiatrices des côtés \([AB]\) et \([BC]\).
Le point \(O\) est un point de la médiatrice du segment \([AB]\), donc \(OA=OB\).
Le point \(O\) est un point de la médiatrice du segment \([BC]\), donc \(OB=OC\).
Ainsi \(OA=OB=OC\). Le point \(O\) est aussi sur la médiatrice du segment \([AC]\).
Le point \(O\) est équidistant de \(A\), de \(B\) et de \(C\), les trois sommets du triangle.
Le cercle de centre \(O\) et de rayon \(OA\) passe par les trois points \(A\), \(B\) et \(C\) : c'est le cercle circonscrit au triangle.