Déterminer la mesure d'un angle
Méthode :
En utilisant les angles de figures connues (triangle isocèle, équilatéral, carré...).
Méthode :
En utilisant les propriétés d'angles particuliers :
Exemple :
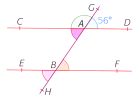
Les droites \((CD)\) et \((EF)\) sont parallèles.
Déterminer les mesures des angles : \(\widehat{GBF}\) ; \(\widehat{CAB}\) ; \(\widehat{EBH}\) et \(\widehat{GAC}\).
Comme les droites \((CD)\) et \((EF)\) sont parallèles,
les angles correspondants \(\widehat{BAD}\) et \(\widehat{GBF}\) ont la même mesure. Donc \(\widehat{GBF}=56°\).
Comme les droites \((CD)\) et \((EF)\) sont parallèles,
les angles alternes-internes \(\widehat{CAB}\) et \(\widehat{GBF}\) ont la même mesure. Donc \(\widehat{CAB}=56°\).
Comme \(\widehat{EBH}\) et \(\widehat{GBF}\) sont opposés par le sommet,
ils ont la même mesure. Donc \(\widehat{EBH}=56°\).
Comme \(\widehat{GAC}\) et \(\widehat{GAD}\) sont supplémentaires, \(\widehat{GAC}=180°-56°=124°\).
Méthode :
En utilisant la propriété de la somme des angles d'un triangle.