Aire d'un triangle
Propriété :
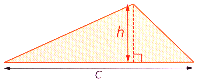
L'aire \(\mathcal{A}\) d'un triangle est la moitié du produit de la longueur \(c\) d'un de ses côtés par la hauteur \(h\) relative à ce côté.
\[\mathcal{A}=\dfrac{c\times h}{2}\]
Exemple :
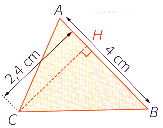
L'aire du triangle \(ABC\) :
On repère un côté et sa hauteur associée et on divise par deux le produit des longueurs :
\(\mathcal{A}=\dfrac{c\times h}{2}=\dfrac{4~cm\times2,4~cm}{2}=4,8~cm^2\)
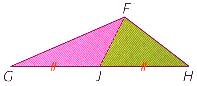
Propriété :
Chaque médiane d'un triangle partage ce triangle en deux triangles de même aire.
Exemple :
Dans le triangles \(FHG\) ci-contre, \((FJ)\) est la médiane issue du sommet \(F\).
Les triangles \(FGJ\) et \(FJH\) ont la même aire.