Écriture fractionnaire d'un quotient
Définition :
Le quotient d'un nombre \(a\) par un nombre \(b\), différent de \(0\), est le nombre par lequel il faut multiplier \(b\) pour obtenir \(a\).
On le note \(a:b\) ou en écriture fractionnaire \(\dfrac{a}{b}\).
\(\dfrac{a}{b}\times b=a\) avec \(b\neq0\)
Exemples :
\(\dfrac{12}{4}\) est le quotient de \(12\) par \(4\) ; il est égal à \(3\).
En effet, \(3\times4=12\), donc \(\dfrac{12}{4}=3\). (Dans ce cas, le quotient est un nombre entier.)
\(\dfrac{3,5}{5}\) est le quotient de \(3,5\) par \(5\) ; il est égal à \(0,7\).
En effet, \(0,7\times5=3,5\), donc \(\dfrac{3,5}{5}=0,7\). (Dans ce cas, le quotient est un nombre décimal.)
\(\dfrac{4}{3}\) est le quotient de \(4\) par \(3\) ; ce n'est pas un nombre décimal car la division ne se termine pas.
En effet, \(4:3\approx1,33\) ou \(1,33\times3\approx4\) donc \(\dfrac{4}{3}\approx1,33\).
Définition :
Si \(a\) et \(b\) désignent deux nombres, avec \(b\) non nul :
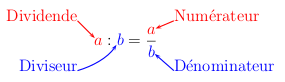
Si les nombres \(a\) et \(b\) sont entiers, le quotient \(\frac{a}{b}\) est appelé une fraction.
Si la fraction \(\dfrac{a}{b}\) est égale à un nombre entier, on dit que :
\(a\) est un multiple de \(b\) ;
\(b\) est un diviseur de \(a\) ;
\(a\) est divisible par \(b\).