Notions de fonctions
Définition :
Le processus qui à un nombre fait correspondre un unique nombre s'appelle une fonction. On peut présenter une fonction sous trois formes : algébrique (expression algébrique), numérique (tableau de valeurs) ou graphique (représentation graphique).

Exemple :
On considère le programme de calcul suivant :
choisir un nombre compris entre 0 et 7 ;
élever ce nombre au carré ;
soustraire ce nombre de 49 ;
prendre la racine carrée du résultat ;
multiplier cette racine carrée par le nombre choisi au départ ;
annoncer le résultat final.
Ce programme de calcul permet de définir une fonction notée \(f\).
Voici trois modes de représentation de cette fonction \(f\) :
Définition : Expression algébrique
\(f:x\longmapsto x\times\sqrt{49-x^2}\)
Le nombre \(x\) est l'antécédent de \(x\times\sqrt{49-x^2}\).
Le nombre \(x\times\sqrt{49-x^2}\) est l'image de \(x\) par la fonction \(f\). On note \(f(x)=x\times\sqrt{49-x^2}\).
Définition : Tableau de valeurs
Le tableau de valeurs est formé de quelques valeurs de \(x\) (pour un tableau partiel) et de leurs images respectives par la fonction \(f\).
\(x\) | 1 | 2 | 3 | 4 |
\(f(x)\) | 3 | 8 | 15 | 24 |
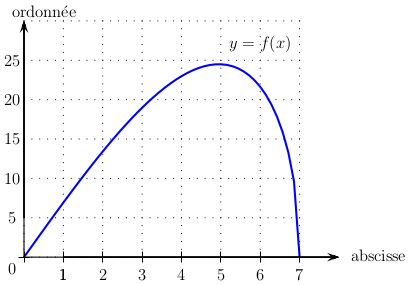
Définition : Représentation graphique
La représentation graphique de \(f\) est l'ensemble des points de coordonnées \(\big(x;f(x)\big)\). \(\big(\)couples (antécédents ; images)\(\big)\).