Fonction linéaire
Définition : Expression algébrique
Soit \(a\) un nombre fixé.
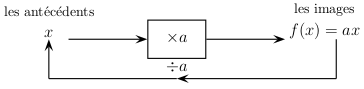
Le procédé \(f : x \longmapsto ax\), qui au nombre \(x\) associe le nombre \(ax\) s'appelle une fonction linéaire.
Exemple :
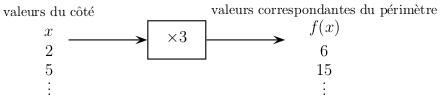
Le procédé associant le côté d'un triangle équilatéral à son périmètre définit une fonction linéaire de coefficient 3.
Propriété : Tableau de valeurs
Un tableau de valeurs associé à une fonction linéaire \(f(x)=ax\) est un tableau de proportionnalité de coefficient \(a\).
Exemple du périmètre du triangle équilatéral en fonction de son côté :
longueur du côté | 2 | 3 | 4 | 5 |
périmètre du triangle équilatéral | 6 | 9 | 12 | 15 |
Propriété : Représentation graphique
Une fonction linéaire décrit une situation de proportionnalité, elle est donc associée à une droite passant par l'origine. Dans un repère, la représentation graphique de la fonction linéaire de coefficient \(a\) est la droite qui passe par l'origine O du repère et par les points de coordonnées \((x ; ax)\).
Conséquence :
Pour tracer la représentation graphique d'une fonction linéaire il suffit de connaître un nombre et son image, l'origine étant toujours un point de cette représentation.
Définition :
On dit que \(y=ax\) est une équation de la droite qui représente graphiquement la fonction linéaire de coefficient linéaire \(a\). \(a\) est appelé le coefficient directeur de cette droite.
Exemple :
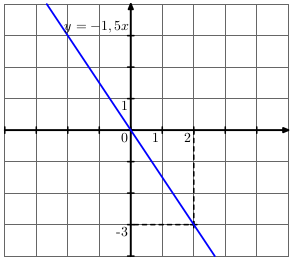
Représentation graphique de \(f : x \longmapsto-1,5x\)
Calcul d'une image en choisissant un antécédent : avec \(2\) comme antécédent \((x=2)\), l'image est \(f(2)=-1,5\times2=-3\)
La fonction \(f\) est une fonction linéaire, sa représentation est donc un droite qui passe par l'origine et le point de coordonnées \((2;-3)\).