Fonction affine
Définition : Expression algébrique
Soient \(a\) et \(b\) deux nombres fixés.
Le procédé \(f : x \longmapsto ax+b\), qui au nombre \(x\) associe le nombre \(ax+b\) s'appelle une fonction affine.

Exemple :
La fonction qui au nombre de séances \(x\) associe le prix à payer (en €) \(f(x)\) dans une tarification où l'abonnement coûte 40 € et la séance 2 € est exprimée par la relation : \(f:x\longmapsto 2x+40\).
\(f(4)=2\times4+40=48\) Pour 4 séances, le prix à payer est de 48 €.
\((56-40)\div2=8\) Avec 56 €, je peux aller à 8 séances.
Propriété : Représentation graphique
Dans un repère, la représentation graphique de la fonction affine est une droite qui passe par les points de coordonnées \((x ; ax+b)\).
Conséquence :
Pour tracer la représentation graphique d'une fonction affine il suffit de connaître deux nombres et leurs images respectives.
Définition :
On dit que \(y=ax+b\) est une équation de la droite qui représente graphiquement la fonction affine.
\(a\) est appelé le coefficient directeur de cette droite.
\(b\) est appelé l'ordonnée à l'origine de cette droite.
Exemple :
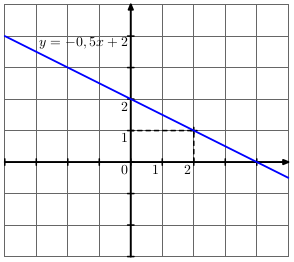
Représentation graphique de \(f :x \longmapsto -0,5x+2\)
Calculs de deux images en choisissant deux antécédents différents :
Pour \(x=0\), \(f(0)=-0.5\times0+2=2\).
Pour \(x=2\), \(f(2)=-0,5\times2+2=1\).
La fonction \(f\) est une fonction affine, sa représentation est donc un droite. D'après les calculs précédents, elle passe par les points de coordonnées \((0;2)\) et \((2;1)\).
Remarque :
Comme pour les fonctions linéaires, le coefficient influence la direction de la droite.
Propriété : Proportionnalité des accroissements
Soit \(f : x \longmapsto ax+b\) une fonction affine.
Il y a proportionnalité entre les accroissements des images \(f(x)\) et les accroissements des antécédents \(x\).
On a : \(\frac{f(x_2)-f(x_1)}{x_2-x_1}=a\).
Interprétation graphique :
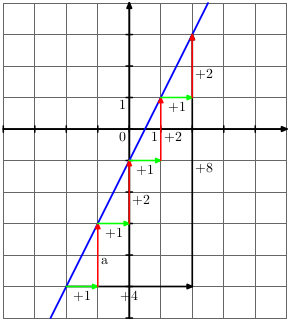
\(f : x \longmapsto 2x-1\)
Si la différence des abscisses est de \(+4\), celle des ordonnées est de \(2\times (+4)=(+8)\) où \(2\) est le coefficient de la fonction.
Si la différence des abscisses est de \(+1\), celle des ordonnées est de \(a\times (+1)=a\). On retrouve ainsi le coefficient \(a\) de la fonction.
Remarque :
Connaissant deux nombres et leurs images par une fonction affine, cette propriété permet de calculer rapidement \(a\) et d'en exprimer, par la suite (après avoir déterminé \(b\)), son expression algébrique complète.