L'inégalité triangulaire

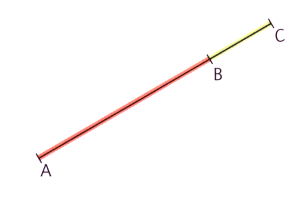
Le plus court chemin entre deux points est la ligne droite. Tout autre chemin, passant par un troisième point, est plus long ou égal. En conséquence, on peut énoncer la propriété admise suivante :

Propriété

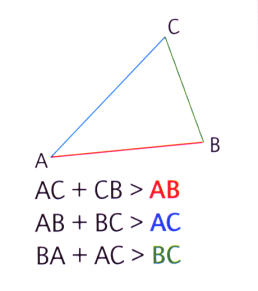
Si \(A\), \(B\) et \(C\) sont trois points quelconques, alors \(AB+BC\geqslant AC\).

Exemples :

  • Cas d'inégalité : Dans un triangle, la somme des longueurs de deux côtés est supérieure à la longueur du troisième côté.

  • Cas d'égalité : L'égalité \(AB+BC=AC\) correspond au cas où le point \(B\) appartient au segment \([AC]\).

Attention ! \(B\) n'est pas nécessairement le milieu du segment \([AC]\).