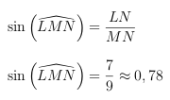Trigonométrie
Définition :
Dans un triangle rectangle :
le cosinus d'un angle aigu est égal au rapport \(\frac{\mbox{longueur du côté adjacent à cet angle}}{\mbox{longueur de l'hypoténuse}}\) ;
le sinus d'un angle aigu est égal au rapport \(\frac{\mbox{longueur du côté opposé à cet angle}}{\mbox{longueur de l'hypoténuse}}\) ;
la tangente d'un angle aigu est égal au rapport \(\frac{\mbox{longueur du côté opposé à cet angle}}{\mbox{longueur du côté adjacent à cet angle}}\).
Exemple :
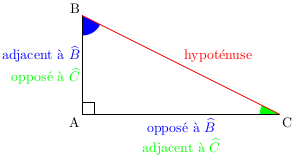
\(ABC\) est un triangle rectangle en \(A\) donc :
\(\cos\widehat{B}=\dfrac{AB}{BC}\hspace{60pt}\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\sin\widehat{B}=\dfrac{AC}{BC}\hspace{60pt}\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}\hspace{60pt}\tan\widehat{C}=\dfrac{AB}{AC}\)
Remarque :
Le cosinus d'un angle et le sinus d'un angle aigu est toujours compris entre 0 et 1.
Conseil : Moyen Mnémotechnique
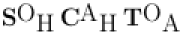
Exemples :
Calcul d'une longueur :
Déterminer une valeur approchée de \(AB\) à \(10^{-1}\) cm près.
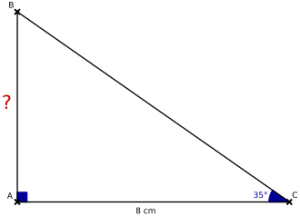
Dans le triangle \(ABC\) rectangle en A :
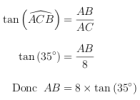(voir la propriété du produit en croix)
Ainsi \(AB\approx5,6\) cm. (Valeur obtenue en utilisant une table trigonométrique ou la calculatrice)
Calcul d'un angle :
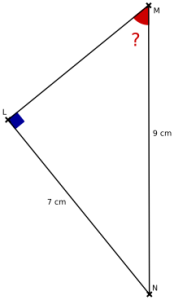
Calculer la mesure de l'angle \(\widehat{LMN}\) au degré près.
Dans le triangle \(LMN\) rectangle en L :
Ainsi \(\widehat{LMN}\approx 51°\) (Valeur obtenue en utilisant une table trigonométrique ou la calculatrice pour déterminer \(\sin^{-1}\left(\frac{7}{9}\right)\)).
Propriété :
\(\alpha\) désigne la mesure d'un angle aigu :
\((\cos\alpha)^2+(\sin\alpha)^2=\cos^2\alpha+\sin^2\alpha=1\hspace{50pt}\mbox{et}\hspace{50pt}\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)