Réciproque du théorème de Thalès
Propriété :
Soit \((d)\) et \((d')\) deux droites sécantes en \(A\).
Si les points \(A\), \(M\) et \(B\) sont alignés dans cet ordre ;
les points \(A\), \(N\) et \(C\) sont alignés dans cet ordre
et \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\) alors les droites \((BC)\) et \((MN)\) sont parallèles.
Remarque :
Cette propriété permet de montrer que deux droites sont parallèles.
Exemple :
Est-ce que les droites \((MN)\) et \((BC)\) sont parallèles ? Justifier.
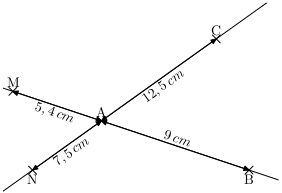
Dans les triangles \(ABC\) et \(AMN\),
les points \(M\), \(A\) et \(B\) sont alignés dans cet ordre ;
les points \(N\), \(A\) et \(C\) sont alignés dans cet ordre ;
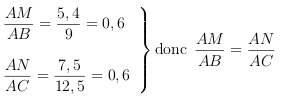
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\) donc d'après la réciproque du théorème de Thalès, les droites \((MN)\) et \((BC)\) sont parallèles.
Remarque :
Le produit en croix peut être utile pour comparer deux quotients.