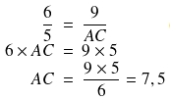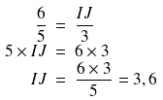Théorème de Thalès
Propriété :
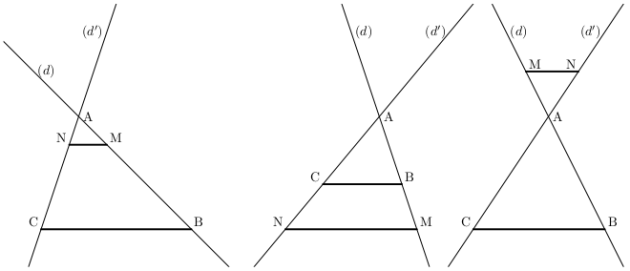
Soit \((d)\) et \((d')\) deux droites sécantes en \(A\).
Les points \(A\), \(B\) et \(M\) sont alignés.
Les points \(A\), \(C\) et \(N\) sont alignés.
Si les droites \((BC)\) et \((MN)\) sont parallèles alors \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\qquad\left(\dfrac{\mbox{côtés du triangle }AMN}{\mbox{côtés correspondants du triangle }ABC}\right)\)
Remarque :
Cette propriété permet de calculer des longueurs connaissant un des rapports.
Exemple :
Les droites \((CJ)\) et \((BI)\) se coupent en \(A\). Les droites \((BC)\) et \((IJ)\) sont parallèles. Calculer les longueurs \(AC\) et \(IJ\).
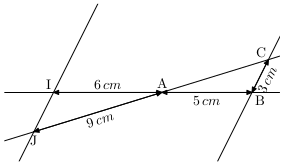
Dans les triangles \(ABC\) et \(AIJ\) :
\(A\), \(I\) et \(B\) sont alignés ;
\(A\), \(J\) et \(C\) sont alignés et
la droite \((IJ)\) est parallèle à la droite \((BC)\).
Donc, d'après le théorème de Thalès, on a \(\dfrac{AI}{AB}=\dfrac{AJ}{AC}=\dfrac{IJ}{BC}\quad\mbox{c'est à dire}\quad\dfrac{6}{5}=\dfrac{9}{AC}=\dfrac{IJ}{3}\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.