Agrandissement et réduction
Définition :
Les longueurs sur une carte, un plan, un dessin " à l'échelle" sont proportionnelles aux longueurs réelles.
L'échelle est le coefficient de proportionnalité entre les distances représentées et les distances réelles, exprimées avec la même unité.
\(\mbox{échelle}=\dfrac{\mbox{distance sur la représentation}}{\mbox{distance réelle}}\) |
Remarque :
Si l'échelle est un nombre inférieur à 1, la reproduction est une réduction par rapport à la réalité (carte, plan de construction, maquette...).
Si l'échelle est un nombre supérieur à 1, la reproduction est un agrandissement par rapport à la réalité (photographie sous microscope).
Exemples :
Sur une carte, 5 cm représentent 100 km, soit 10 000 000 cm.
L'échelle d'une carte s'exprime par une fraction de numérateur 1,
à savoir ici \(\dfrac{5}{10\,000\,000}=\dfrac{1}{2\,000\,000}\)
Un insecte mesure 3 mm de longueur ; on le représente sur un dessin avec une longueur de 6 cm.
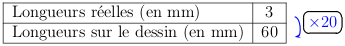
L'échelle du dessin est \(\dfrac{60}{3}=20\).
Propriété :
Lors d'un agrandissement ou d'une réduction d'un objet à l'échelle \(k\) :
les longueurs de l'objet sont multipliées par \(k\) ;
l'aire de la surface de l'objet est multipliée par \(k^2\) ;
le volume de l'objet est multiplié par \(k^3\).
Exemples :
Deux feuilles de format A4 sont nécessaires pour recouvrir exactement une feuille de format A3 (\(k=\sqrt2\) et \(k^2=2\) soit le double de la surface).
Huit petits cubes d'arête \(a\) sont nécessaires pour remplir un cube d'arête \(2a\) (\(k=2\) et \(k^3=8\)).
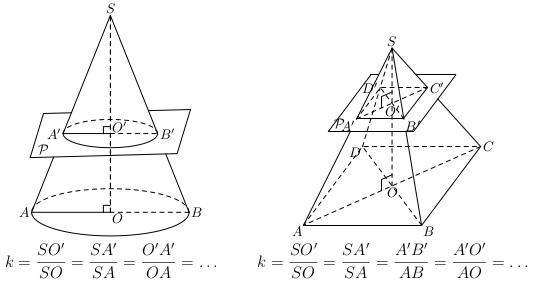
La section d'une pyramide (ou d'un cône de révolution) par un plan parallèle à la base est une réduction de la base de la pyramide (ou du cône) - voir la section "Pyramide" ou "Cône de révolution" -. Le rapport de réduction \(k\) est égal au quotient d'une longueur de la petite pyramide ou du petit cône par la longueur correspondante de la pyramide ou du cône de départ. (Le rapport d'agrandissement est l'inverse de celui de réduction).