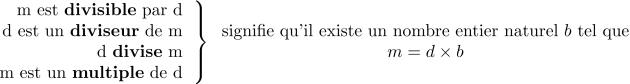Multiple et diviseurs
Définition :
Un entier naturel est un nombre entier positif ou nul.
Exemple :
\(8\) est un diviseur de \(112\) car \(112=8\times 14\).
Pour la même raison, \(14\) est un diviseur de \(112\).
Remarque :
\(1\) est un diviseur de tout nombre entier \(a\) car \(a=1\times a\).
Un nombre entier \(a\) est aussi son propre diviseur car \(a=1\times a\).
Propriété : Critères de divisibilité
Un entier est divisible par 2 s'il est pair, donc lorsque son chiffre des unités est 0, 2, 4, 6 ou 8.
Un entier est divisible par 4 lorsque le nombre formé par son chiffre des dizaines et son chiffre des unités est divisible par 4.
Un entier est divisible par 3 lorsque la somme de ses chiffres est divisible par 3.
Un entier est divisible par 9 lorsque la somme de ses chiffres est divisible par 9.
Un entier est divisible par 5 lorsque son chiffre des unités est 0 ou 5.
Un entier est divisible par 10 lorsque son chiffre des unités est 0.
Exemples :
\(120\) est divisible par \(4\) car \(20\) est un multiple de \(4\).
\(276\) est un multiple de \(3\) car \(2+7+6=15\) et \(15\) est divisible par \(3\).
\(2\,439\) a \(9\) pour diviseur car \(2+4+3+9=18\) et \(18\) est un multiple de \(9\).