Gérer une situation de proportionnalité
Principe : Dès que l'on connaît deux nombres qui se correspondent, on peut déterminer à partir d'une troisième valeur la quatrième, appelée la quatrième proportionnelle.
Exemple :
Un marcheur se déplace à une allure régulière. Il parcourt 400 m en 5 min. Dans ces conditions, il y a proportionnalité entre la durée du parcours et la distance parcourue.
Méthode : Multiplier les quantités
400 m en 5 min donc en 10 min (2 fois plus) il parcourt 2 fois plus de distance soit 800 m.

Méthode : Additionner des quantités
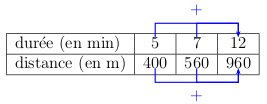
400 m en 5 min et 560 m en 7 min donc il parcourt au total $400m+560m=960m$ en 12 min.
Méthode : Passer par l'unité
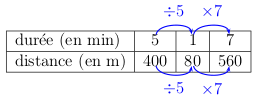
400m en 5 min donc 80 m en 1 min (5 fois moins)
ainsi il parcourt 560 m en 7 min (7 fois plus qu'en 1 min).
Méthode : Utiliser le coefficient de proportionnalité
400 m en 5 min or \(5\times{\color{blue}{80}}=400\) donc en 13 min, il parcourt \(13\times{\color{blue}{80}}=1040~m\).

Méthode : Utiliser le produit en croix
Dans le tableau de proportionnalité ci-dessous, le produit en croix permet d'obtenir la quatrième proportionnelle :
\(400\times8=5\times x\).
Donc \(x=\dfrac{400\times8}{5}=640\).
